密钥协商算法简介

密钥协商算法主要有三类：

（1）依靠非对称加密算法

（2）依靠专门的密钥交换算法

（3）依靠通讯双方事先已经共享的秘密（如PSK）等

DH，Diffie-Hellman算法

Diffie-Hellman密钥交换（Diffie-Hellman key exchange）是1976年由Whitfield Diffie和Martin Hellman共同发明的一种算法。使用这种算法，通信双方仅通过交换一些可以公开的信息就能生成出共享的对称密码的密钥。虽然这种算法叫“密钥交换”，但是实际上并没有真正的交换密钥，而是通过计算生成出了一个相同的共享密钥。准确的来说，应该叫Diffie-Hellman密钥协商（Diffie-Hellman key agreement）。

DH协商算法的过程如下：

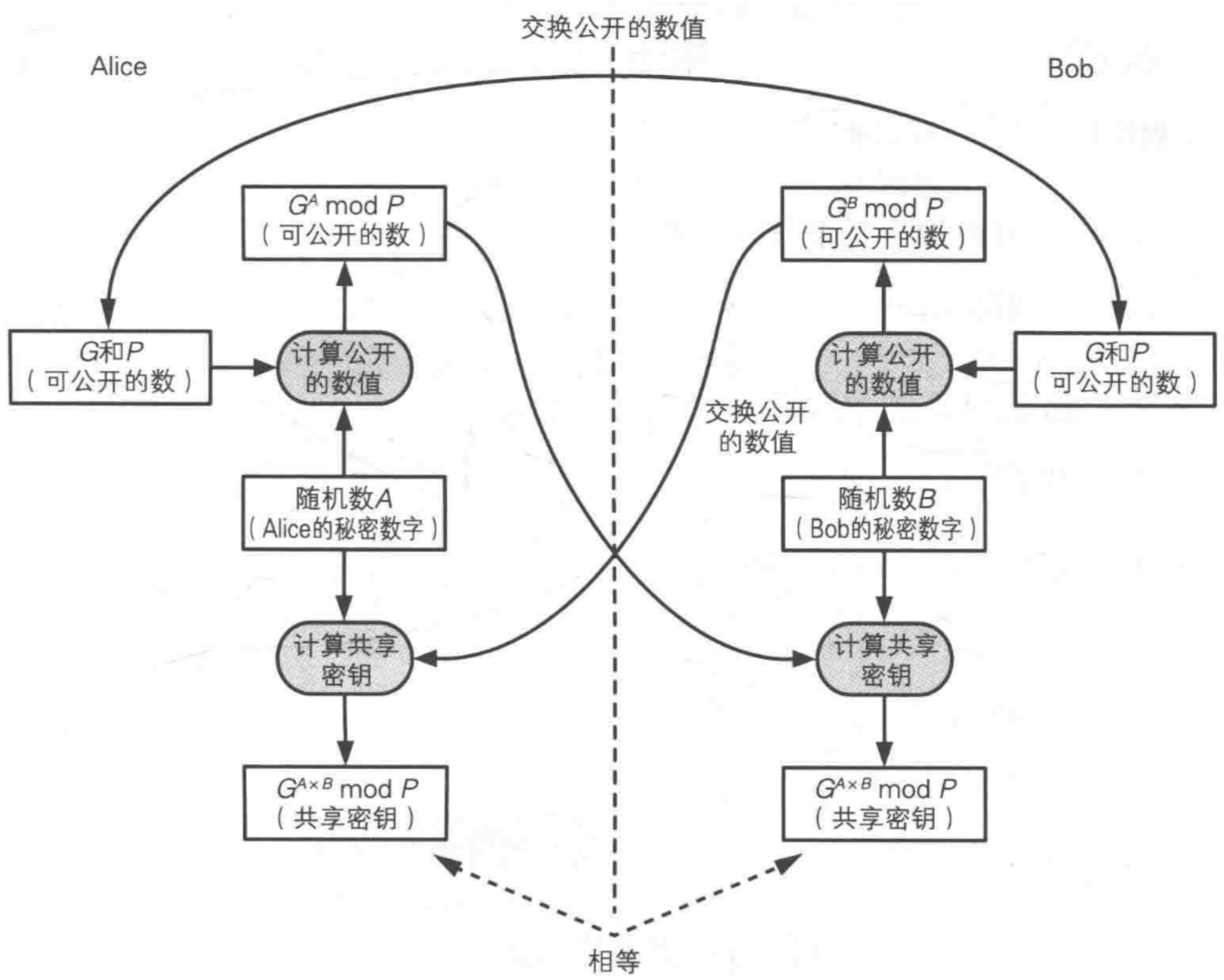
（1）Alice向Bob发送两个质数P和G

P是一个非常大的质数，G是一个较小的数字，称为生成元。P和G可以公开，P和G的生成也可以由任何一方生成。

（2）Alice生成一个随机数A

A是1~(P-2)之间的整数，这个数只有Alice知道。

（3）Bob生成一个随机数B

B是1~(P-2)之间的整数，这个数只有Bob知道。

（4）Alice把(G^A mod P)的结果发送给Bob

这个数被窃听了也没有关系。

（5）Bob把(G^B mod P)的结果发送给Alice

这个数被窃听了也没有关系。

（6）Alice用Bob发过来的数计算A次方并求mod P

这个数就是最终的共享密钥，如下：

(G^B mod P)^A mod P = G^(B*A) mod P = G^(A*B) mod P

（7）Bob用Alice发过来的数计算B次方并求mod P

这个数就是最终的共享密钥，如下：

(G^A mod P)^B mod P = G^(A*B) mod P

至此，A和B计算出来的密钥是一致的。

窃听者能获取到的信息有P、G、G^A mod P、G^B mod P。通过这4个值想计算出G^(A*B) mod P是非常困难的。

如果能知道A和B任意一个数，就可以破解上面所有步骤，并算出最后的共享密钥。但是窃听者只能获取到G^A mod P、G^B mod P，这里的mod P是关键，如果是知道G^A也可以算出A，但是这里是推算不出A和B的，因为这是有限域(finite field)上的离散对数问题。

使用DH算法，即使协商过程中被别人全程偷窥（比如“网络嗅探”），偷窥者也【无法】知道协商得出的密钥是啥。但是DH算法本身也有缺点，即不支持数字认证。也就是无法对抗中间人攻击MITM，因为缺乏身份认证，必定会遭到中间人攻击。为了避免遭遇MITM攻击，DH需要与其它签名算法（比如RSA、DSA、ECDSA）配合，靠签名算法帮忙来进行身份认证。当DH与RSA配合使用，称之为DH-RSA，与DSA配合则称为DH-DSA，以此类推。反之，如果DH没有配合某种签名算法，则称为DH-ANON（ANON是洋文“匿名”的简写），此时会遭遇中间人攻击/MITM。

使用RSA作为密钥协商算法

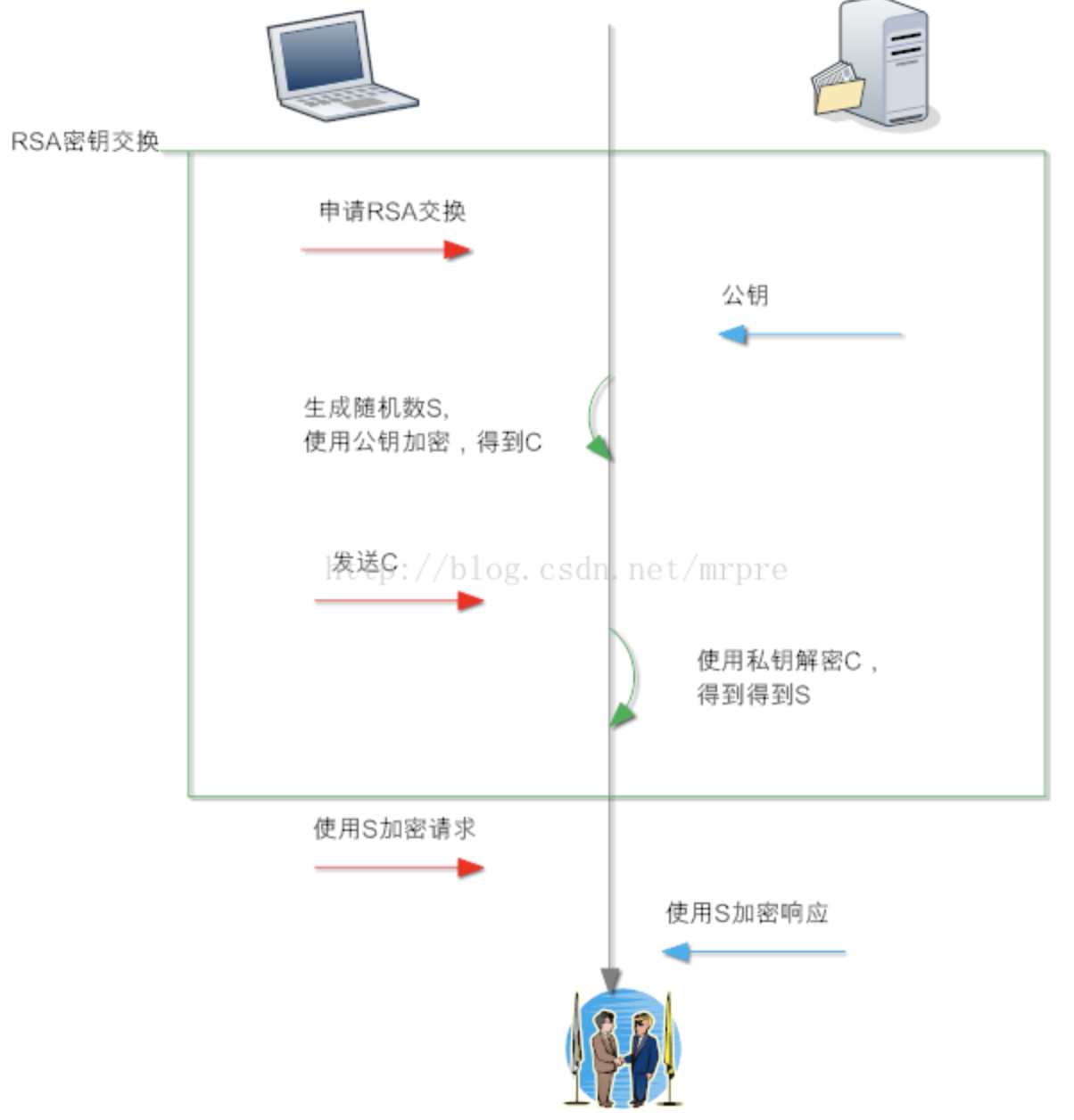
RSA算法流程文字描述如下：

（1）任意客户端对服务器发起请求，服务器首先发回复自己的公钥到客户端（公钥明文传输）。

（2）客户端使用随机数算法，生成一个密钥S，使用收到的公钥进行加密，生成C，把C发送到服务器。

（3）服务器收到C，使用公钥对应的私钥进行解密，得到S。

（4）上述交换步骤后，客户端和服务器都得到了S，S为密钥（预主密钥）。

使用DHE密钥协商算法

DHE是DH的扩展。

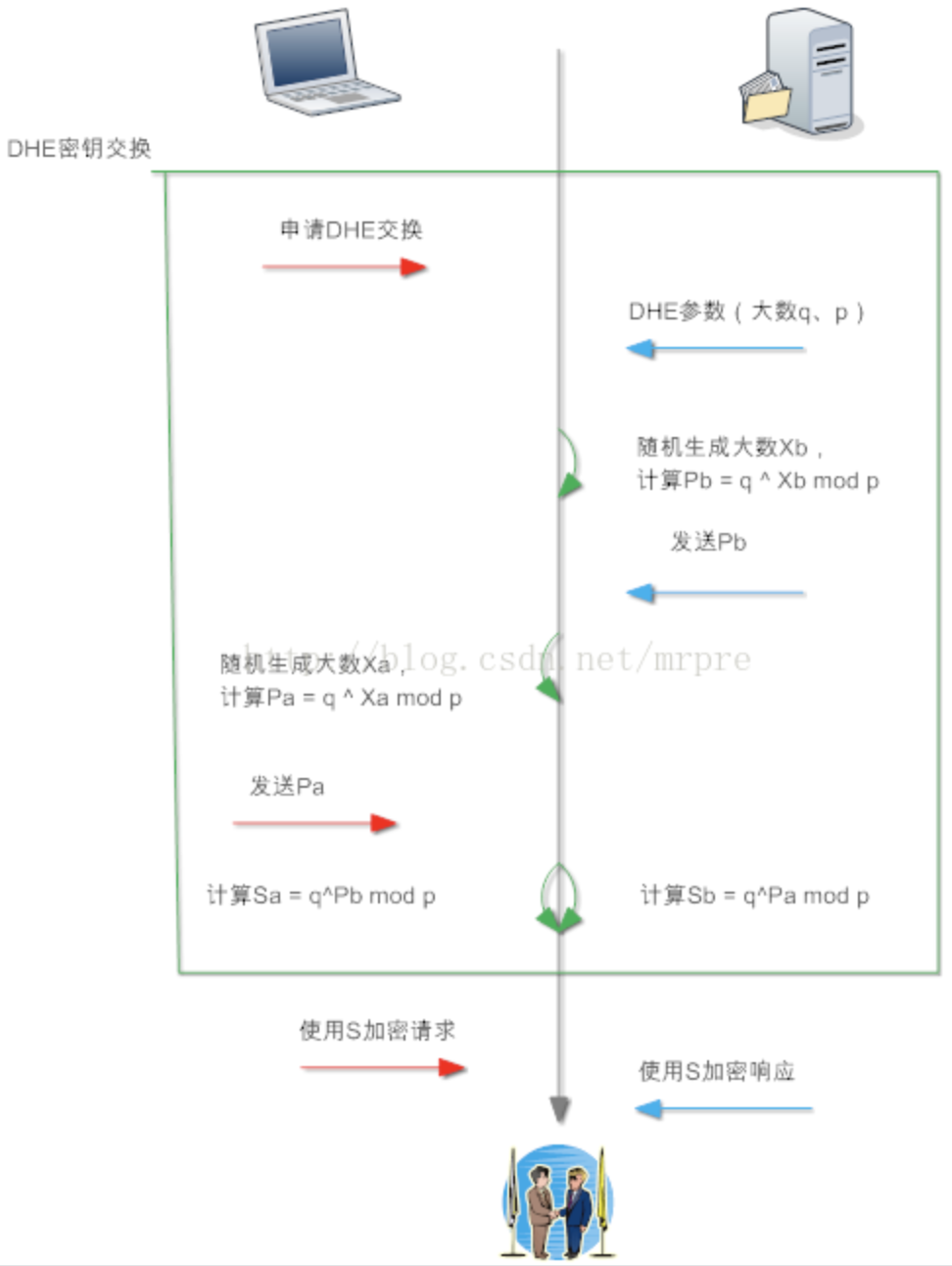
DHE算法流程文字描述如下：

（1）客户端计算一个随机值Xa，使用Xa作为指数，即计算Pa = q^Xa mod p，其中q和p是全世界公认的一对值。客户端把Pa发送至服务器，Xa作为自己私钥，仅且自己知道。

（2）服务器和客户端计算流程一样，生成一个随机值Xb，使用Xb作为指数，计算Pb = q^Xb mod p，将结果Pb发送至客户端，Xb仅自己保存。

（3）客户端收到Pb后计算Sa = Pb ^Xa mod p；服务器收到Pa后计算Sb = Pa^Xb mod p

（4）算法保证了Sa = Sb = S，故密钥交换成功，S为密钥（预主密钥）

使用ECDHE密钥协商算法

ECDHE是基于椭圆曲线EC的DHE密钥协商算法。

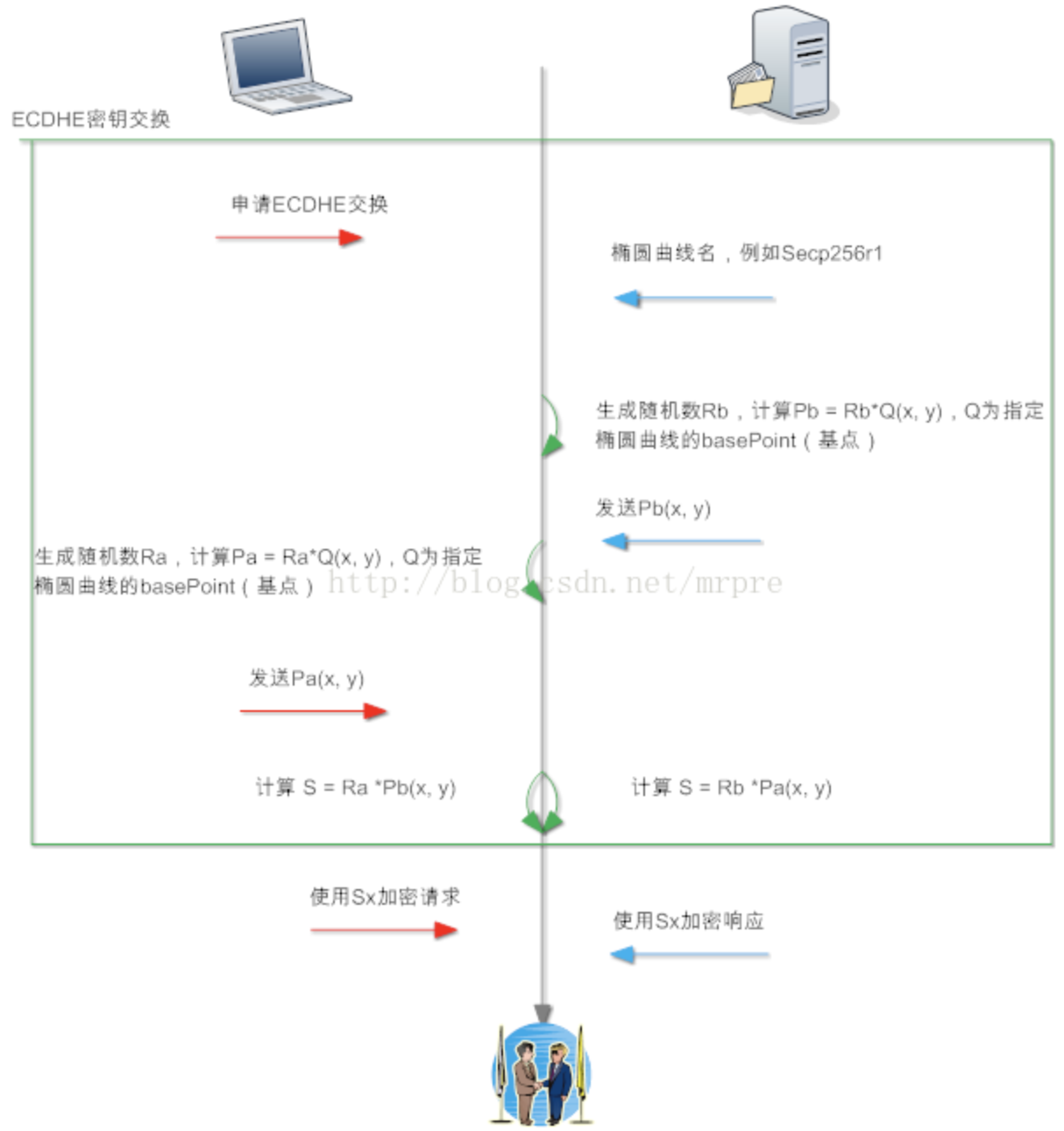
ECDHE算法流程文字描述如下：

（1）客户端随机生成随机值Ra，计算Pa(x, y) = Ra * Q(x, y)，Q(x, y)为全世界公认的某个椭圆曲线算法的基点。将Pa(x, y)发送至服务器（其中Pa(x, y)相当于客户端的公钥）

备注：根据椭圆曲线，由xG和G不能推算出x，也就有Pa(x,y)和Q(x,y)无法推算出来随机数Ra。

（2）服务器随机生成随机值Rb，计算Pb(x,y) = Rb * Q(x, y)。将Pb(x, y)发送至客户端（其中Pb(x, y)相当于客户端的公钥）

（3）客户端计算Sa(x, y) = Ra * Pb(x, y)；服务器计算Sb(x, y) = Rb * Pa(x, y)

（4）算法保证了Sa = Sb = S，提取其中的S的x向量作为密钥（预主密钥）

备注：根据椭圆曲线性质可知，获取到Pb(x,y)和Pa(x,y)，是无法计算出对应的随机数Ra或Rb的。随意窃听者拿到公开的信息后，是根本无法计算出对称加密阶段的密钥的，所以很安全。

学习资料参考于：
https://halfrost.com/cipherkey/
https://blog.csdn.net/mrpre/article/details/78025940
https://program-think.blogspot.com/2016/09/https-ssl-tls-3.html