椭圆曲线密码学

ECC，全称为Elliptic Curve Cryptography，中文名为椭圆曲线密码学，是一种基于椭圆曲线数学的非对称加密算法。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。ECC的主要优势是在某些情况下它比其他的算法（比如RSA加密算法）使用更小的密钥并提供相当的或更高等级的安全。

椭圆曲线可以用于3个方面：一类是基于椭圆曲线的公钥密码；一类是基于椭圆曲线的数字签名；一类是基于椭圆曲线的密钥交换。

目前比较常用的两个曲线是P-256（secp256r1，在OpenSSL称为prime256v1）和x25519。P-256是NIST（美国国家标准技术研究所）和NSA（美国国家安全局）推荐使用的曲线，而x25519被认为是最安全、最快速的曲线。但密码学界普遍不信任NIST和NSA，所以一般都使用x25519。

椭圆曲线

椭圆曲线下图所示：

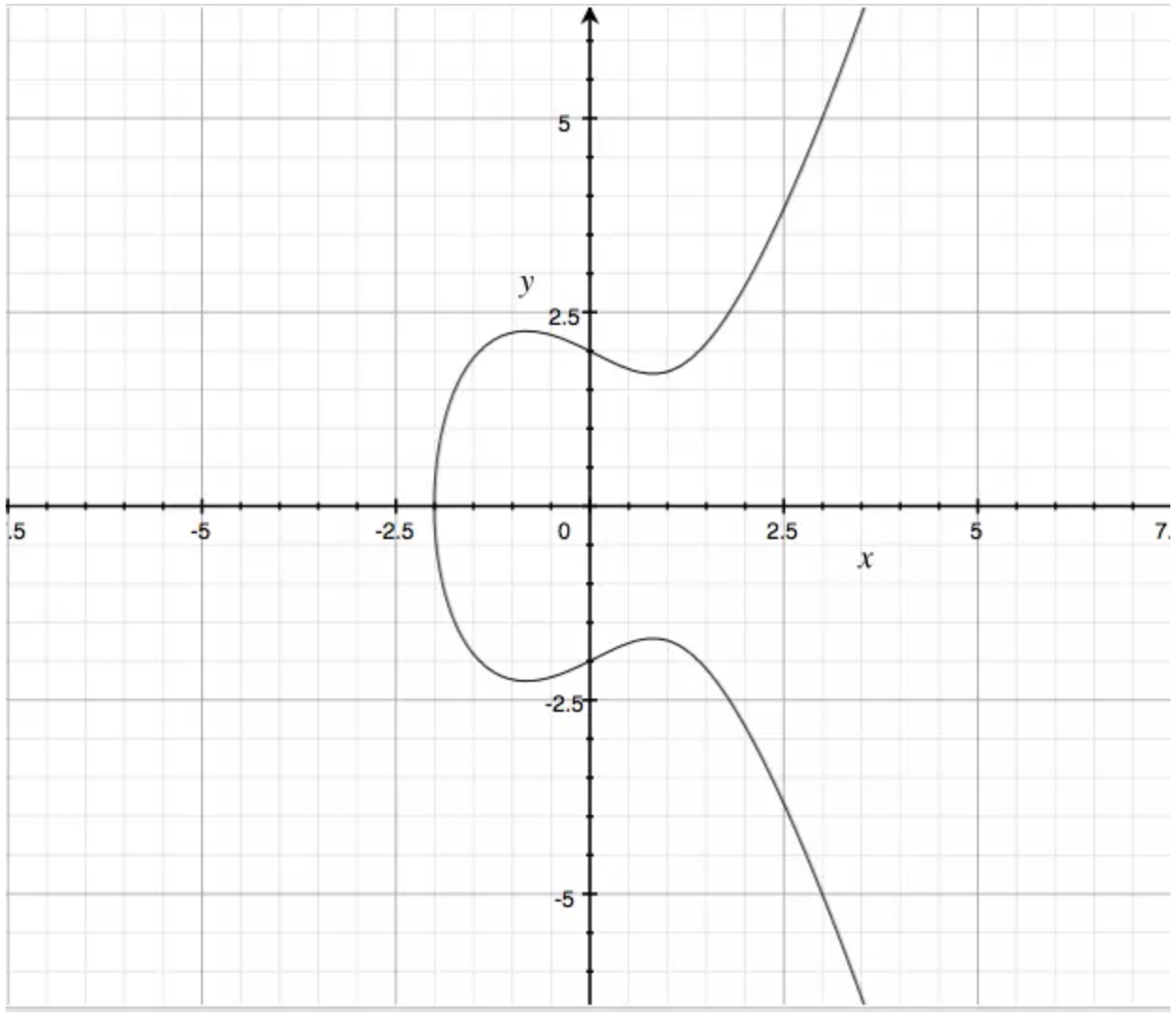
现在，我们来定义椭圆曲线上的加法。现在有椭圆曲线y^2=x^3-x，曲线上的点P和Q。过P和Q做一条直线，交椭圆曲线为点R’,再过R’点做垂直于X轴的直线，交曲线另一点为R，定义P + Q = R。如下图所示：

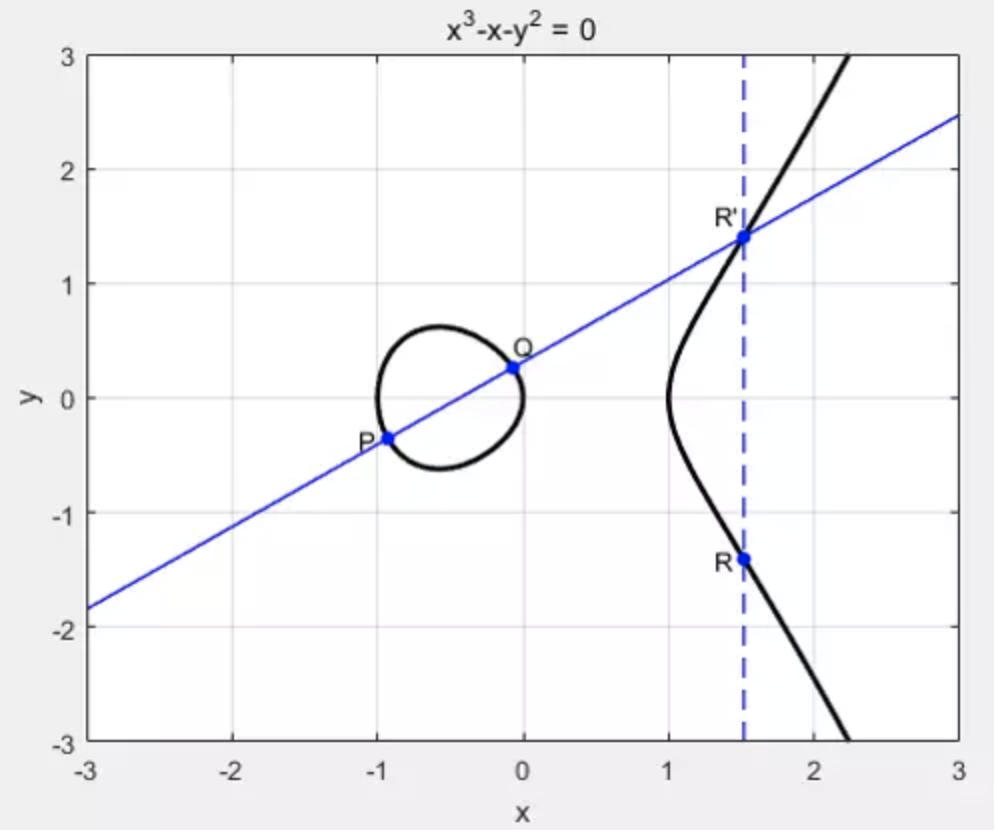
若P=Q,则为过P点的切线交于椭圆曲线为R’。如下图所示：

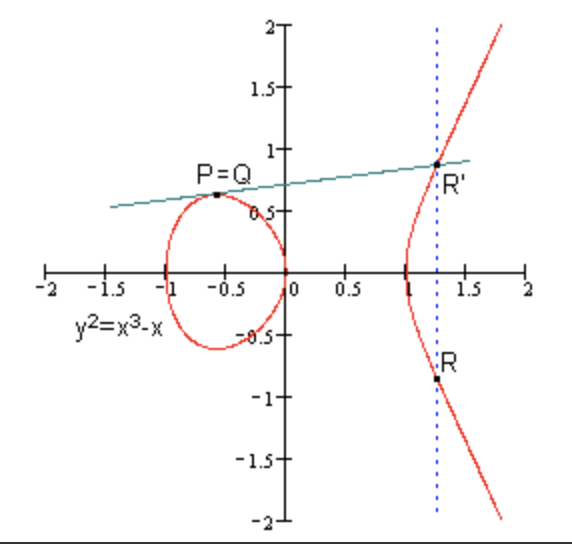
这样，称R = 2P。类似的，3P = P + P + P = P + 2P = P + R。也就是说，当给定点P时，“已知数x求点xG的运算”不难，因为有加法的性质，运算起来可以比较快。但反过来，“已知点xG求x的问题”则非常困难，因为只能遍历每一个x做运算。这就是椭圆曲线密码中所利用的“椭圆曲线上的离散对数问题”。

椭圆曲线密码利用了上述“运算”中的“椭圆曲线上的离散对数问题”的复杂度，就像RSA利用了“大数质因数分解”的复杂度，以及EIGamal密码的Diffie-Hellman密钥交换利用了“有限域上的离散对数问题”的复杂度一样。

椭圆曲线上的离散对数问题：

这个问题的难度保证了椭圆曲线密码的安全性。

椭圆曲线的公钥和私钥

在椭圆曲线加密中，给定椭圆曲线E，基点G和点xG，我们称xG为公钥，x值为私钥。由椭圆曲线性质可知，已知私钥求公钥很简单，而已知公钥求私钥几乎是不可能的事情。

学习资料参考于：
https://halfrost.com/asymmetric_encryption/
https://juejin.im/post/5a67f3836fb9a01c9b661bd3